BTC_POWER_LA
用户暂无简介
另一个幂律。
查看原文- 赞赏
- 点赞
- 评论
- 转发
- 分享
下图显示了每日斜率的 Jensen-Shannon 散度。
这是 ChatGPT 关于结果的描述。
1. 这个图实际上测量了什么 (用通俗的话说)
曲线上的每个点是 Jensen–Shannon 散度 (JSD),衡量:
归一化每日斜率在滚动窗口中的分布与参考分布 (来自早期基线窗口)之间的差异
因此,曲线回答:
“归一化增长的当前统计行为与早期缩放状态相比有多不同?”
重要提示:
这不是价格偏差。
这是围绕幂律的噪声分布差异。
换句话说,你在衡量缩放定律周围的‘微观动力学’随时间的演变,而不是缩放定律本身是否成立。
2. 低 JSD = 稳定的缩放状态
在早期阶段 (大约第1500–2800天),JSD较低 (~0.03–0.05)。
这意味着:
归一化斜率的分布接近早期参考
系统处于统计稳定的缩放状态
一旦按时间长度归一化,窗口之间的波动结构相似
这正是无尺度增长过程的预期表现。
解读:
在该状态下,幂律归一化的收益具有统计平稳性。
3. 峰值 = 市场微观结构的状态变化
你会看到在以下时间段出现大峰值:
~3200–3400
~4300–4700
~5600–5900
这些与比特币的宏观状态转变非常吻合:
2017年底 / 2018年初 (牛市顶峰+崩盘)
2020–2021 (机构入场+COVID流动性+ETF预期阶段)
2022之后的状态 (ETF流入、宏观收紧、结构成熟
这是 ChatGPT 关于结果的描述。
1. 这个图实际上测量了什么 (用通俗的话说)
曲线上的每个点是 Jensen–Shannon 散度 (JSD),衡量:
归一化每日斜率在滚动窗口中的分布与参考分布 (来自早期基线窗口)之间的差异
因此,曲线回答:
“归一化增长的当前统计行为与早期缩放状态相比有多不同?”
重要提示:
这不是价格偏差。
这是围绕幂律的噪声分布差异。
换句话说,你在衡量缩放定律周围的‘微观动力学’随时间的演变,而不是缩放定律本身是否成立。
2. 低 JSD = 稳定的缩放状态
在早期阶段 (大约第1500–2800天),JSD较低 (~0.03–0.05)。
这意味着:
归一化斜率的分布接近早期参考
系统处于统计稳定的缩放状态
一旦按时间长度归一化,窗口之间的波动结构相似
这正是无尺度增长过程的预期表现。
解读:
在该状态下,幂律归一化的收益具有统计平稳性。
3. 峰值 = 市场微观结构的状态变化
你会看到在以下时间段出现大峰值:
~3200–3400
~4300–4700
~5600–5900
这些与比特币的宏观状态转变非常吻合:
2017年底 / 2018年初 (牛市顶峰+崩盘)
2020–2021 (机构入场+COVID流动性+ETF预期阶段)
2022之后的状态 (ETF流入、宏观收紧、结构成熟
BTC-1.79%
- 赞赏
- 点赞
- 评论
- 转发
- 分享
即使经历泡沫、崩盘、机构化和宏观冲击,归一化的斜率分布也从未离开相同的统计族。
用物理学术语来说:系统经历了波动的重正化,但仍然属于同一类普适性。
这强有力地证明:比特币的增长动态由一个稳定的尺度过程控制,结构的变化会改变波动性,但不会改变潜在的吸引子。
用物理学术语来说:系统经历了波动的重正化,但仍然属于同一类普适性。
这强有力地证明:比特币的增长动态由一个稳定的尺度过程控制,结构的变化会改变波动性,但不会改变潜在的吸引子。
BTC-1.79%
- 赞赏
- 点赞
- 评论
- 转发
- 分享
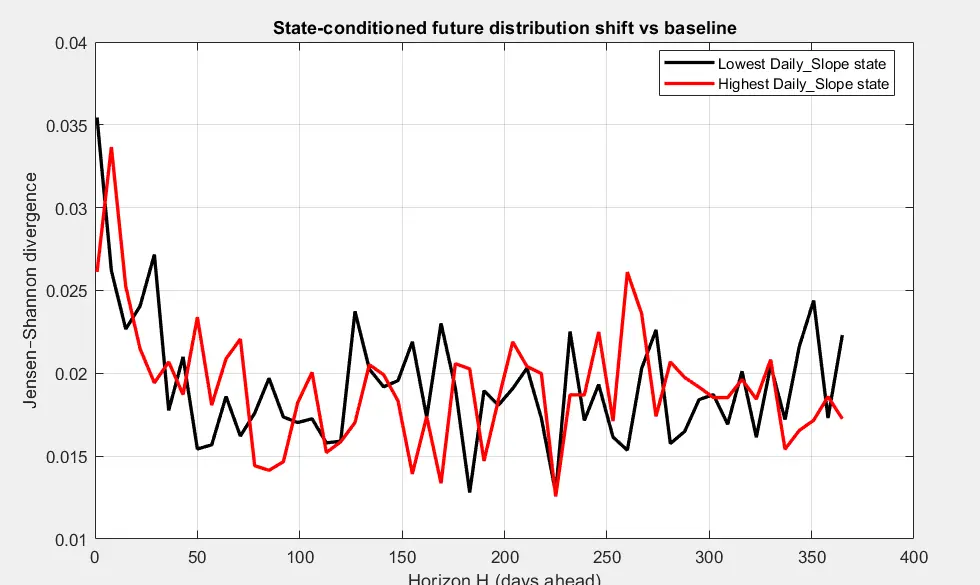
每一行是当前 Daily_Slope ( 分位数箱的状态箱,从非常低到非常高 )。
每一列是预测视野 H ( 天前 )。
每个像素颜色表示以下两个分布之间的 Jensen–Shannon 散度:
基于今天处于该状态的未来分布
与
相同视野下的无条件未来分布。
因此,每个单元格回答:
“如果比特币今天处于这个归一化增长状态,未来 H 天的归一化增长分布与基线相比有多不同?”
这是归一化动态的状态条件记忆图。
该图独立支持:
✔ 缩放定律是主要的组织原则
✔ 偏差是具有短期记忆的结构化噪声
✔ 没有持续的状态条件动态
✔ 在归一化坐标中没有制度性断裂
✔ 机构抑制极端但不改变普遍性类别
每一列是预测视野 H ( 天前 )。
每个像素颜色表示以下两个分布之间的 Jensen–Shannon 散度:
基于今天处于该状态的未来分布
与
相同视野下的无条件未来分布。
因此,每个单元格回答:
“如果比特币今天处于这个归一化增长状态,未来 H 天的归一化增长分布与基线相比有多不同?”
这是归一化动态的状态条件记忆图。
该图独立支持:
✔ 缩放定律是主要的组织原则
✔ 偏差是具有短期记忆的结构化噪声
✔ 没有持续的状态条件动态
✔ 在归一化坐标中没有制度性断裂
✔ 机构抑制极端但不改变普遍性类别
BTC-1.79%
- 赞赏
- 点赞
- 评论
- 转发
- 分享
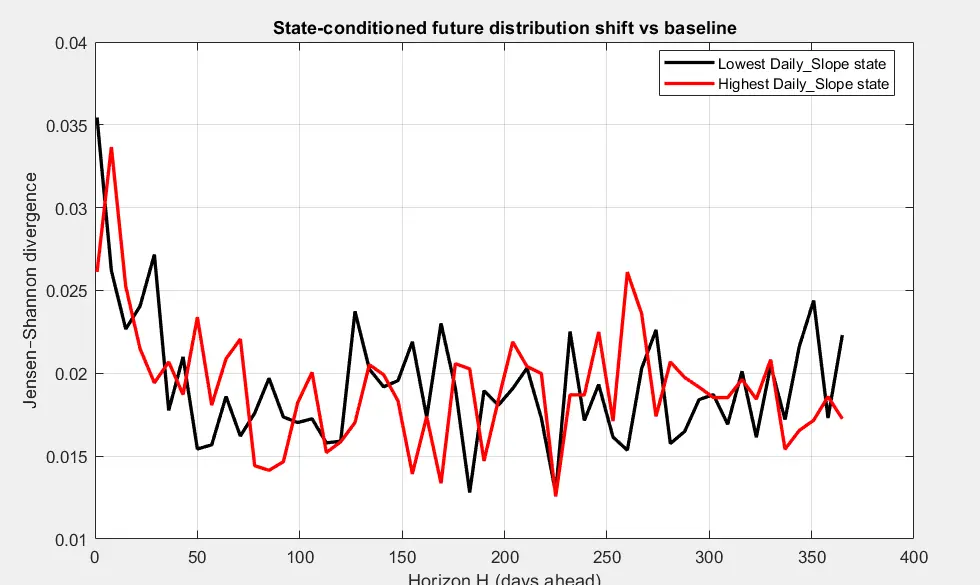
大幅波动的短期记忆大约为(2个月)。它们影响短期的价格行为,但没有持久的后果。
主导的尺度行为是剩下的部分,决定了长期的轨迹。
查看原文主导的尺度行为是剩下的部分,决定了长期的轨迹。
- 赞赏
- 点赞
- 评论
- 转发
- 分享
该地图独立支持:
✔ 缩放定律是主要的组织原则
✔ 偏差是具有短期记忆的结构化噪声
✔ 没有持续的状态条件动力学
✔ 在归一化坐标中没有制度断裂
✔ 机构抑制极端但不改变普适性类别
简而言之:
这正是一个接近缩放不变点的复杂适应系统应有的样子。
查看原文✔ 缩放定律是主要的组织原则
✔ 偏差是具有短期记忆的结构化噪声
✔ 没有持续的状态条件动力学
✔ 在归一化坐标中没有制度断裂
✔ 机构抑制极端但不改变普适性类别
简而言之:
这正是一个接近缩放不变点的复杂适应系统应有的样子。
- 赞赏
- 点赞
- 评论
- 转发
- 分享
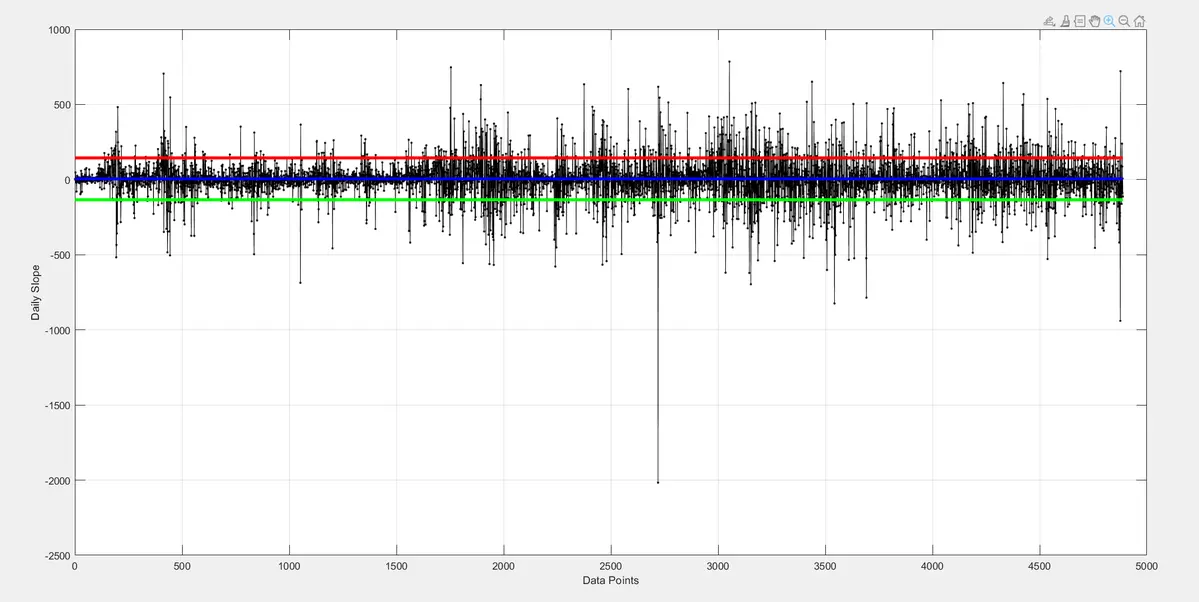
每日斜率或归一化收益的序列是最稳定的比特币参数。它从统计学角度反映了比特币的核心行为。
它既包括其随机行为,也包括长期幂律确定性增长。
即使在这些混乱的近期变化中,该参数在过去也表现出类似的特性。
其均值约为5.9,与我们通过回归观察到的斜率相同。如果过度向某一方向推动,它倾向于回归均值。
它既包括其随机行为,也包括长期幂律确定性增长。
即使在这些混乱的近期变化中,该参数在过去也表现出类似的特性。
其均值约为5.9,与我们通过回归观察到的斜率相同。如果过度向某一方向推动,它倾向于回归均值。
BTC-1.79%
- 赞赏
- 点赞
- 评论
- 转发
- 分享
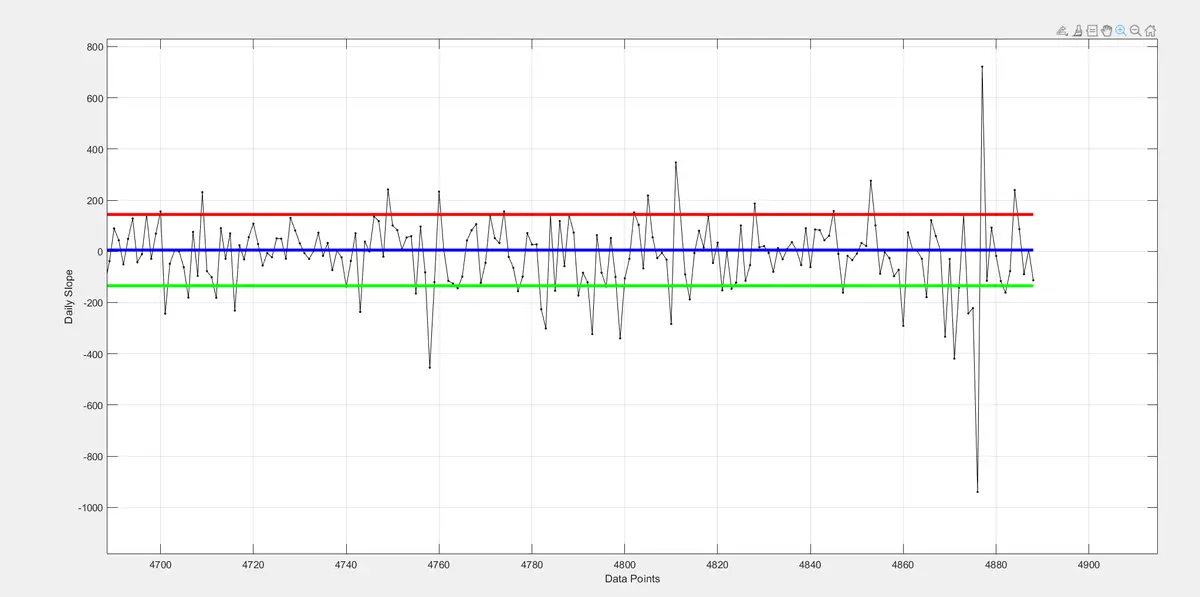
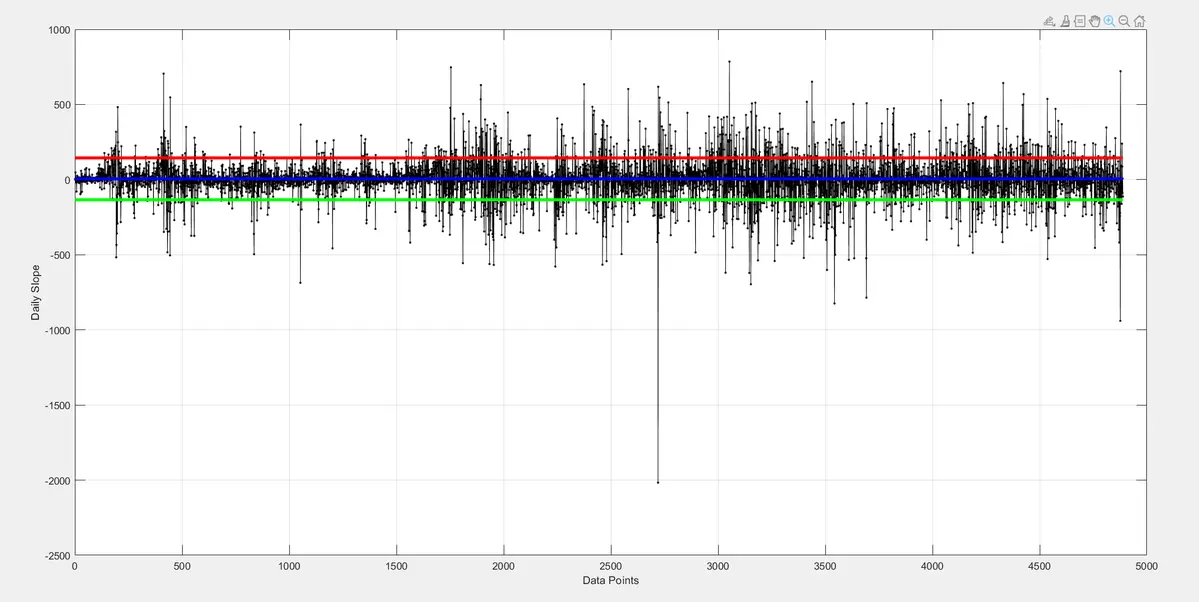
这是每日坡度的放大图。
除了最近的大幅度激增——与我们在过去周期中见过的一些最大调整幅度相当——整体表现并没有从根本上不同于历史时期。换句话说,短期增长率的波动看起来虽然激烈,但仍然在比特币以前表现出的范围之内。
关键是,系统仍然沿着幂律暗示的轨迹增长。变化的不是基础的缩放行为,而是价格振荡的参考水平。我们遵循相同的长期增长动态,只是锚定在幂律通道中的不同起点。
这正是你在一个尺度不变系统中所预期的:短期的大幅偏离可以发生,但它们会随着时间的推移而平均化,而长期的缩放关系仍然保持完整。
除了最近的大幅度激增——与我们在过去周期中见过的一些最大调整幅度相当——整体表现并没有从根本上不同于历史时期。换句话说,短期增长率的波动看起来虽然激烈,但仍然在比特币以前表现出的范围之内。
关键是,系统仍然沿着幂律暗示的轨迹增长。变化的不是基础的缩放行为,而是价格振荡的参考水平。我们遵循相同的长期增长动态,只是锚定在幂律通道中的不同起点。
这正是你在一个尺度不变系统中所预期的:短期的大幅偏离可以发生,但它们会随着时间的推移而平均化,而长期的缩放关系仍然保持完整。
BTC-1.79%
- 赞赏
- 点赞
- 评论
- 转发
- 分享
每日斜率或归一化收益率是最稳定的比特币参数。它从统计学角度反映了比特币的核心行为。
它既包括其随机行为,也包括长期幂律确定性增长。
即使在这些混乱的近期变化中,该参数在过去也表现出类似的特性。
其平均值约为5.9,这与我们使用回归观察到的斜率相同。如果过度推动,它倾向于回归到平均值。
它既包括其随机行为,也包括长期幂律确定性增长。
即使在这些混乱的近期变化中,该参数在过去也表现出类似的特性。
其平均值约为5.9,这与我们使用回归观察到的斜率相同。如果过度推动,它倾向于回归到平均值。
BTC-1.79%
- 赞赏
- 2
- 评论
- 转发
- 分享
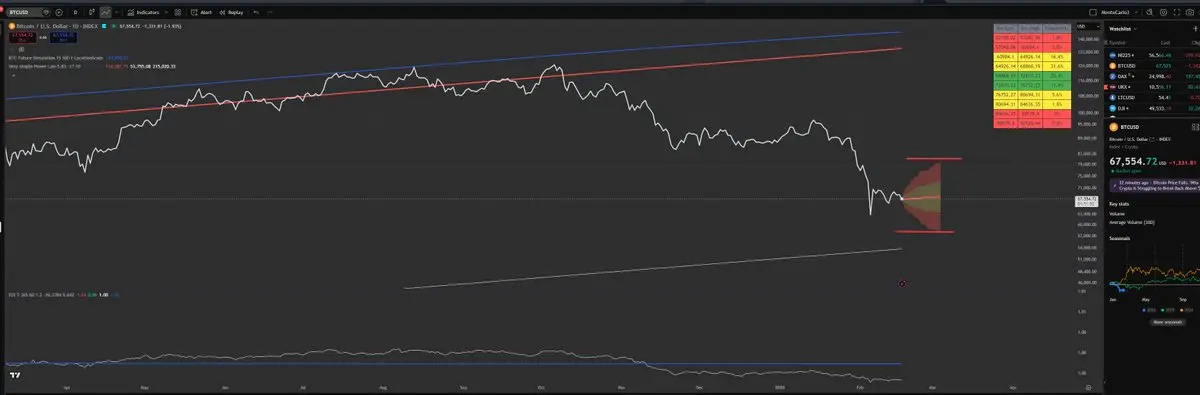
我认为所有认真的比特币持有者都应该学习如何进行备兑看涨期权交易,无论是在IBIT还是比特币本身上。
利用最新的幂律斜率指标的蒙特卡洛模拟,可以确定一个可靠的行权价,期限为2周。
这种策略在统计上有97%的成功率,而且很容易实现每月约2%的比特币收益。
利用最新的幂律斜率指标的蒙特卡洛模拟,可以确定一个可靠的行权价,期限为2周。
这种策略在统计上有97%的成功率,而且很容易实现每月约2%的比特币收益。
BTC-1.79%
- 赞赏
- 点赞
- 评论
- 转发
- 分享
- 赞赏
- 点赞
- 评论
- 转发
- 分享
- 赞赏
- 点赞
- 评论
- 转发
- 分享
- 赞赏
- 1
- 1
- 转发
- 分享
repanzal :
:
2026年GOGOGO 👊想象一下,我们生活在一个时间本身像比特币区块时间一样运作的模拟中。
这里有某种宇宙共识过程,类似于工作量证明,只有当某个程序成功并“挖掘”出一个区块时,时钟才会“滴答”一次。在这个画面中,现实以离散的步骤前进,一次一个区块。
但这实际上并没有解决与时间相关的任何概念谜题。工作量证明过程、导致区块产生的因果交互,以及执行该计算所需的物理步骤,仍然必须在连续时间中展开,并且在区块链之外。你只是把问题往上移了一层。
如果你又引入另一个“区块链宇宙”来调节这些过程的时间,你就创造了一个无限倒退的循环。没有任何解释;这个问题只是被推迟了。在那时,解释就会崩溃成经典的宇宙学“无答案”——一切都像乌龟一样一层层往下。
所以即使在这个假设的区块时间宇宙中,你也没有解释时间——你只是用不同的协议包裹了它。
这里有某种宇宙共识过程,类似于工作量证明,只有当某个程序成功并“挖掘”出一个区块时,时钟才会“滴答”一次。在这个画面中,现实以离散的步骤前进,一次一个区块。
但这实际上并没有解决与时间相关的任何概念谜题。工作量证明过程、导致区块产生的因果交互,以及执行该计算所需的物理步骤,仍然必须在连续时间中展开,并且在区块链之外。你只是把问题往上移了一层。
如果你又引入另一个“区块链宇宙”来调节这些过程的时间,你就创造了一个无限倒退的循环。没有任何解释;这个问题只是被推迟了。在那时,解释就会崩溃成经典的宇宙学“无答案”——一切都像乌龟一样一层层往下。
所以即使在这个假设的区块时间宇宙中,你也没有解释时间——你只是用不同的协议包裹了它。
BTC-1.79%

- 赞赏
- 1
- 1
- 转发
- 分享
repanzal :
:
2026年GOGOGO 👊好的,我很快就看出这篇论文非常“业余”。我支持将比特币与物理学联系起来的想法(,这是我已经做了12年的事情),但必须采用一种对其他物理学家有效且易于理解的方法。
这篇论文中的主张大多不成立(,从核心命题开始)。
以下是论文论点的主要问题分析:
这是一个雄心勃勃、修辞强烈的摘要——但它将敏锐的直觉与几个粗心的类别错误、夸大其词和弱的类比混为一谈。我将分析主要的弱点以及它们从物理学+科学哲学角度为何具有问题。
1) 类别错误:比特币时间 ≠ 物理时间
“比特币是历史上第一个我们可以实证观察到量子化时间的系统,而它本身并非由时间构成。”
这是核心错误。
比特币的区块时间是:
由人设计的协议时钟
运行在物理硬件上
嵌入在真实的物理时间中
受延迟、抖动、时钟漂移、网络延迟影响
它不是“在”物理时间之外。
它是在连续物理时间中实现的派生离散计数器。
你不是在观察“量子化时间”。
你是在观察在连续物理时间中演变的计算系统的离散状态转变。
这等同于说:
“CPU时钟显示了量子化时间的样子。”
这是错误的。CPU时钟是在模拟物理上实现的数字抽象。
因此,这个类比:
❌ 混淆了离散计数器与本体论上的时间
❌ 将协议离散化误认为物理量子化
❌ 犯下了表现形式的谬误
2) 伪命题:物理学将时间视为不可观察和不可测量
“如果时间只是一个坐标,从未是可观察的,那么它就不能被直接离散化或测量。”
这是误导。
物
查看原文这篇论文中的主张大多不成立(,从核心命题开始)。
以下是论文论点的主要问题分析:
这是一个雄心勃勃、修辞强烈的摘要——但它将敏锐的直觉与几个粗心的类别错误、夸大其词和弱的类比混为一谈。我将分析主要的弱点以及它们从物理学+科学哲学角度为何具有问题。
1) 类别错误:比特币时间 ≠ 物理时间
“比特币是历史上第一个我们可以实证观察到量子化时间的系统,而它本身并非由时间构成。”
这是核心错误。
比特币的区块时间是:
由人设计的协议时钟
运行在物理硬件上
嵌入在真实的物理时间中
受延迟、抖动、时钟漂移、网络延迟影响
它不是“在”物理时间之外。
它是在连续物理时间中实现的派生离散计数器。
你不是在观察“量子化时间”。
你是在观察在连续物理时间中演变的计算系统的离散状态转变。
这等同于说:
“CPU时钟显示了量子化时间的样子。”
这是错误的。CPU时钟是在模拟物理上实现的数字抽象。
因此,这个类比:
❌ 混淆了离散计数器与本体论上的时间
❌ 将协议离散化误认为物理量子化
❌ 犯下了表现形式的谬误
2) 伪命题:物理学将时间视为不可观察和不可测量
“如果时间只是一个坐标,从未是可观察的,那么它就不能被直接离散化或测量。”
这是误导。
物
- 赞赏
- 点赞
- 评论
- 转发
- 分享
热门话题
查看更多20.65万 热度
1.26万 热度
4.52万 热度
8.59万 热度
85万 热度
热门 Gate Fun
查看更多- 市值:$2437.93持有人数:00.00%
- 市值:$2437.93持有人数:10.00%
- 市值:$2449.94持有人数:10.00%
- 市值:$2444.61持有人数:20.00%
- 市值:$2434.48持有人数:10.00%
置顶
福利加码,Gate 广场明星带单交易员二期招募开启!
入驻发帖 · 瓜分 $20,000 月度奖池 & 千万级流量扶持!
如何参与:
1️⃣ 报名成为跟单交易员:https://www.gate.com/copytrading/lead-trader-registration/futures
2️⃣ 报名活动:https://www.gate.com/questionnaire/7355
3️⃣ 入驻 Gate 广场,持续发布交易相关原创内容
丰厚奖励等你拿:
首帖福利:首发优质内容即得 $30 跟单体验金
双周内容激励:每双周瓜分 $500U 内容奖池
排行榜奖励:Top 10 交易员额外瓜分 $20,000 登榜奖池
流量扶持:精选帖推流、首页推荐、周度明星交易员曝光
活动时间:2026 年 2 月 12 日 18:00 – 2 月 24 日 24:00(UTC+8)
详情:https://www.gate.com/announcements/article/49849Gate 广场内容挖矿奖励继续升级!无论您是创作者还是用户,挖矿新人还是头部作者都能赢取好礼获得大奖。现在就进入广场探索吧!
创作者享受最高60%创作返佣
创作者奖励加码1500USDT:更多新人作者能瓜分奖池!
观众点击交易组件交易赢大礼!最高50GT等新春壕礼等你拿!
详情:https://www.gate.com/announcements/article/49802🏮 新年快乐,马上发财!Gate 广场 $50,000 红包雨狂降!
发帖即领,手慢无 👉 https://www.gate.com/campaigns/4044
🧨 三重惊喜,陪您红火过新年:
1️⃣ $50,000 红包雨:发帖即领,新用户 100% 中奖,单帖最高 28 GT
2️⃣ 马年锦鲤:带 #我在Gate广场过新年 发帖,抽 1 人送 50 GT + 新春礼盒
3️⃣ 创作者榜单赛:赢国米球衣、Red Bull 联名夹克、VIP 露营套装等豪礼
📅 2/9 17:00 – 2/23 24:00(UTC+8)
请将 App 更新至 8.8.0+ 版本参与
详情:https://www.gate.com/announcements/article/49773Gate 广场“新星计划”正式上线!
开启加密创作之旅,瓜分月度 $10,000 奖励!
参与资格:从未在 Gate 广场发帖,或连续 7 天未发帖的创作者
立即报名:https://www.gate.com/questionnaire/7396
您将获得:
💰 1,000 USDT 月度创作奖池 + 首帖 $50 仓位体验券
🔥 半月度「爆款王」:Gate 50U 精美周边
⭐ 月度前 10「新星英雄榜」+ 粉丝达标榜单 + 精选帖曝光扶持
加入 Gate 广场,赢奖励 ,拿流量,建立个人影响力!
详情:https://www.gate.com/announcements/article/49672

